LA PASSATEMPO

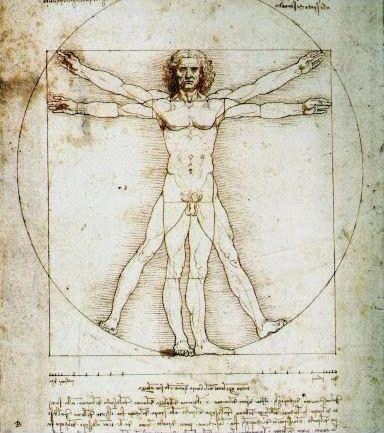
Есть такое понятие -«золотое сечение», формула жизни, графическое изображение которого является спираль Фибоначчи. Спи-раль, выражается «фи»-соотношением, и была широко известна ещё в древности. Её смысл в обнаружении принципов, на которых основаны красота и порядок в природе. Множество растений и моллюсков развиваются по этой пропорции. Она использовалась при сооружении Пирамид и Парфенона, её изучали великие мастера Возрождения – Леонардо да Винчи и Рафаэль. За эстетические свойства этой пропорции было присвоено наименование «золотого сечения» или «божественной пропорции».

Золотое сечение имеет множество замечательных свойств, но ещё больше свойств вымышленных. Многие люди «стремятся найти» золотое сечение во всём, что между полутора и двумя. Под «правилом золотого сечения» в архитектуре и искусстве обычно понимается асимметричные композиции, не обязательно содержащие золотое сечение

Начиная с Леонардо да Винчи, многие художники сознательно использовали пропорции «золотого сечения».

Пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона якобы свидетельствуют, что египетские мастера пользовались соотношениями золотого сечения при их создании.Принято считать, что понятие о золотом сечении ввел в научный обиход Пифагор.

Есть предположение, что Пифагор свое знание позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. В 1855 г. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд «Эстетические исследования».
Цейзинг измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение выражает средний статистический закон.

Цейзинг дал определение золотому сечению, показал, как оно выражается в отрезках прямой и в цифрах. Когда цифры, выражающие длины отрезков, были получены, Цейзинг увидел, что они составляют ряд Фибоначчи.

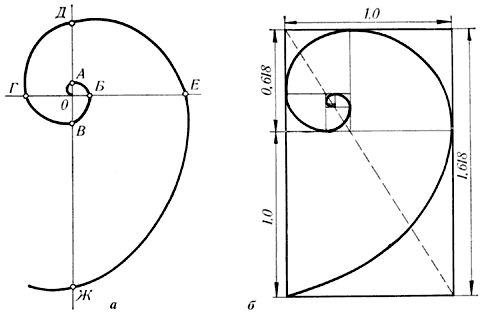
Ряд чисел 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д. известен как ряд Фибоначчи. Особенность последовательности чисел состоит в том, что каждый ее член, начиная с третьего, равен сумме двух предыдущих 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13, 8 + 13 = 21; 13 + 21 = 34 и т.д., а отношение смежных чисел ряда приближается к отношению золотого деления.

Так, 21 : 34 = 0,617, а 34 : 55 = 0,618. (или 1.618, если делить большее число на меньшее).

Ряд Фибоначчи мог бы остаться только математическим казусом, если бы не то обстоятельство, что все исследователи золотого деления в растительном и в животном мире, не говоря уже об искусстве, неизменно приходили к этому ряду как арифметическому выражению закона золотого сечения.

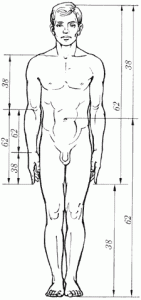
Деление тела точкой пупа – важнейший показатель золотого сечения. Пропорции мужского тела колеблются в пределах среднего отношения 13 : 8 = 1,625 и несколько ближе подходят к золотому сечению, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8 : 5 = 1,6.

У новорожденного пропорция составляет отношение 1 : 1, к 13 годам она равна 1,6, а к 21 году равняется мужской.
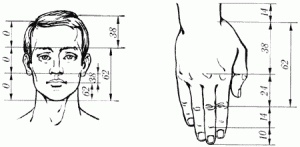
Пропорции золотого сечения проявляются и в отношении других частей тела – длина плеча, предплечья и кисти, кисти и пальцев и т.д.
Справедливость своей теории Цейзинг проверял на греческих статуях. Наиболее подробно он разработал пропорции Аполлона Бельведерского. Подверглись исследованию греческие вазы, архитектурные сооружения различных эпох, растения, животные, птичьи яйца, музыкальные тона, стихотворные размеры.
Еще в 1925 году искусствовед Л.Л.Сабанеев, проанализировав 1770 музыкальных произведений 42 авторов, показал, что подавляющее большинство выдающихся сочинений можно легко разделить на части или по теме, или по интонационному строю, или по ладовому строю, которые находятся между собой в отношении золотого сечения.
В кино С. Эйзенштейн искусственно построил фильм Броненосец Потёмкин по правилам «золотого сечения». Он разбил ленту на пять частей. В первых трёх действие разворачивается на корабле. В двух последних — в Одессе, где разворачивается восстание. Этот переход в город происходит точно в точке золотого сечения. Да и в каждой части есть свой перелом, происходящий по закону золотого сечения.

Еще в 1925 году искусствовед Л.Л.Сабанеев, проанализировав 1770 музыкальных произведений 42 авторов, показал, что подавляющее большинство выдающихся сочинений можно легко разделить на части или по теме, или по интонационному строю, или по ладовому строю, которые находятся между собой в отношении золотого сечения.

Причем, чем талантливее композитор, тем в большем количестве его произведений найдено золотых сечений. У Аренского, Бетховена, Бородина, Гайдна, Моцарта, Скрябина, Шопена и Шуберта золотые сечения найдены в 90% всех произведений. По мнению Сабанеева, золотое сечение приводит к впечатлению особой стройности музыкального сочинения.

В кино С. Эйзенштейн искусственно построил фильм Броненосец Потёмкин по правилам «золотого сечения». Он разбил ленту на пять частей. В первых трёх действие разворачивается на корабле. В двух последних — в Одессе, где разворачивается восстание. Этот переход в город происходит точно в точке золотого сечения. Да и в каждой части есть свой перелом, происходящий по закону золотого сечения.

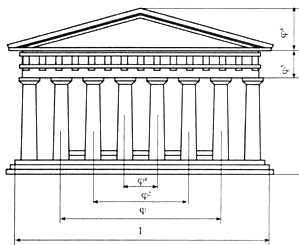
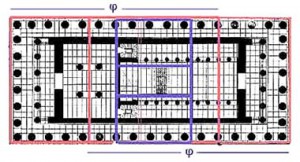
Одним из красивейших произведений древнегреческой архитектуры является Парфенон (V в. до н. э.).

На рисунках виден целый ряд закономерностей, связанных с золотым сечением. Пропорции здания можно выразить через различные степени числа Ф=0,618…

На плане пола Парфенона также можно заметить «золотые прямоугольники»:

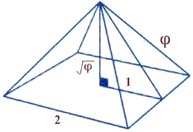
Золотое соотношение мы можем увидеть и в здании собора Парижской Богоматери (Нотр-дам де Пари), и в пирамиде Хеопса:

Не только египетские пиpамиды постpоены в соответствии с совеpшенными пpопоpциями золотого сечения; то же самое явление обнаpужено и у мексиканских пиpамид.

Золотая пропорция применялась многими античными скульпторами. Известна золотая пропорция статуи Аполлона Бельведерского: рост изображенного человека делится пупочной линией в золотом сечении.

Переходя к примерам “золотого сечения” в живописи, нельзя не остановить своего внимания на творчестве Леонардо да Винчи. Посмотрим внимательно на картину «Джоконда». Композиция портрета построена на»золотых треугольниках».

В шрифтах и бытовых предметах, так же присутствует принцип «Золотого сечения».

В биологических исследованиях было показано, что, начиная с вирусов и растений и кончая организмом человека, всюду выявляется золотая пропорция, характеризующая соразмерность и гармоничность их строения. Золотое сечение признано универсальным законом живых систем.

Было установлено, что числовой ряд чисел Фибоначчи характеризует структурную организацию многих живых систем. Например, винтовое листорасположение на ветке составляет дробь (число оборотов на стебле/число листьев в цикле, напр. 2/5; 3/8; 5/13), соответствующую рядам Фибоначчи.

Хорошо известна «золотая» пропорция пятилепестковых цветков яблони, груши и многих других растений. Носители генетического кода — молекулы ДНК и РНК — имеют структуру двойной спирали; ее размеры почти полностью соответствуют числам ряда Фибоначчи.

Гете подчеркивал тенденцию природы к спиральности.

Паук плетет паутину спиралеобразно. Спиралью закручивается ураган. Испуганное стадо северных оленей разбегается по спирали.

Гете называл спираль «кривой жизни». Спираль увидели в расположении семян подсолнечника, в шишках сосны, ананасах, кактусах и т.д.

Цветки и семена подсолнуха, ромашки, чешуйки в плодах ананаса, хвойных шишках «упакованы» по логарифмическим («золотым») спиралям, завивающимся навстречу друг другу, причем числа «правых «и «левых» спиралей всегда относятся друг к другу, как соседние числа Фибоначчи.

У многих бабочек соотношение размеров грудной и брюшной части тела отвечает золотой пропорции. Сложив крылья, ночная бабочка образует правильный равносторонний треугольник. Но стоит развести крылья, и вы увидите тот же принцип членения тела на 2,3,5,8. Стрекоза также создана по законам золотой пропорции: отношение длин хвоста и корпуса равно отношению общей длины к длине хвоста.

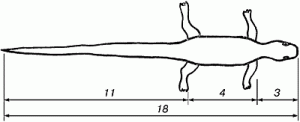
В ящерице длина ее хвоста так относится к длине остального тела, как 62 к 38. Можно заметить золотые пропорции, если внимательно посмотреть на яйцо птицы.

Серебряное сечение — это математическая константа, выражающая некоторое геометрическое соотношение, выделяемое эстетически. В отличие от золотого сечения, по аллюзии с которым оно названо, серебряное сечение не имеет единого определения. (Википедия)

Пропорцию, равную отношению целого к диаметру от целого, условимся называть
СЕРЕБРЯНЫМ СЕЧЕНИЕМ.

феноменом серебряного сечения (то есть с делением прямого отрезка в пропорции длина окружности/диаметр) в природных объектах и в творениях ума, рук и вообще человеческого гения мы сталкиваемся, может быть, не реже, чем с золотым сечением.

По совету Б.В.Раушенбаха, изучением «Серебряного сечения решил заняться, — поэт, писатель и исследователь старины Андрей Чернов на примере системы русских саженей.

Летом 1995 года Андрей Чернов  связался с петербургскими архитекторами-реставраторами, восстанавливавшими храмы Старой Ладоги, и вскоре выяснилось, что в пропорциях Георгиевской и Успенских церквей (обе – XII век) заложено точно такое, как в «Слове о полку Игореве» членение по числу π. С помощью И.Л.Воиновой удалось реконструировать и саму саженную систему. Основана она на корне из двойки, золотом сечении и числе π.

Интересные изыскания были произведены в области литература. Андрей Чернов рассмотрел принцип «Серебряного сечения» на примере произведения Александра Пушкина «Медный всадник».

В «Медном всаднике» 477 строк. Именно строк, а не стихов, что не одно и то же. При этом он, разумеется, не учитывал зачеркнутых самим Пушкиным (трижды!), но восстанавленных в пятом томе Академического издания редактором С.М.Бонди шестнадцати стихов (От «Евгений тут вздохнул сердечно…» по «…И внуки нас похоронят»). Частей в «петербургской повести» три. Каждая больше предыдущей ровно в полтора раза. А если целое разделить на среднюю часть, получится 3,16. Почти что π…

До 3,14 в средней части не хватает одной строки.

Впрочем, в «Медном всаднике» есть  один незарифмованный стих..

Погода пуще свирепела,

Нева вздувалась и ревела,

Котлом клокоча и клубясь,

И вдруг, как зверь остервенясь,

На город кинулась. Пред нею

Все побежало, все вокруг

Вдруг опустело — воды вдруг…

Где рифма к «пред нею»?

Может ее тоже смыло наводнением, как домик Параши?

Андрей Чернов в поиске. Он листает  академическое издание. Есть строка! И в черновике, и в беловой рукописи. Нет ее только в писарской копии, которую Пушкин, впрочем, правил. Бегу в Пушкинский Дом, чтобы свериться с оригиналом беловика:

…Со всею силою своею

Пошла на приступ. Перед нею

Все побежало…

Потерянную писарем строку Пушкин, конечно, заметил. Но восстанавливать не стал. Ведь без нее куда лучше! Так и Нева бросилась на город, смяв расчисленное его  пространство. Пошла на приступ, калеча сам  ритм  жизни  Петрополиса, отменяя законы быта, а заодно и законы рифмовки  четырехстопного ямба.

С восстановленным стихом пропорции «Медного всадника» таковы: Вступление – 96 цельных стихов; часть первая – 148; часть вторая – 222 стиха. Диаметр от 466 стихов как раз и равен 148 стихам. Пропорция по строкам: 97 + 152 + 229 = 478. И при таком подсчете средняя часть равна диаметру всего текста.

Любое художественное творение – виток спирали, разомкнутая окружность. Значит, у композиции стихотворения или фуги может быть и «диаметр композиции». То есть серебряное сечение. Только у Пушкина часть, равная диаметру, посредине поэмы, а у автора «Слова» это две крайние части. Уточним: разница между первой и третьей частями древнерусской поэмы – неполные четыре десятка слогов, но их среднее арифметическое настроено на число π.  Андрей Чернов  вспомнил о древнерусской архитектуре именно потому, что пропорции «Слова» – это пропорции трехнефного крестово-купольного храма. Три части «Слова» – это как три храмовых апсиды:  крайние поменьше, а средняя (алтарная) чуть больше.

Потом, правда, обнаружив акцент серебряного сечения и в других поэмах Пушкина, и в сонетной форме (пятый и десятый стих из четырнадцати), и в фугах Баха, он стал понимать, что невзначай коснулся какой-то закономерности, заложенной в художественную форму самой природой. Объяснение этому Андрей Чернов  видит только в антропоморфности, то есть в человекоподобии, и поэзии, и музыки. Или – что одно и то же! – в космотропности самого человека и наиболее человечных его творений.

Именно на трансцендентном числе π – то есть на таком, которое не может быть получено при помощи алгебраических уравнений! – зиждится гармония самой природы и гармония творчества. Ведь p – основа любой синусоиды, а, значит, и любого гармонического процесса.

Существует одна  СТАРИННАЯ  ОШИБКА КЛАССИЧЕСКОГО МУЗЫКОВЕДЕНИЯ. Если одну октаву (от ноты до и до следующего до) принять за виток спирали, то малая терция будет соответствовать по частоте ноте ля. Но в темперированном (классическом) строе отношение 5/6 уже не работает: камертонное ля равно 440 герцам, а мы по эталонному до II октавы (523,25 герц) получаем ля I октавы в 436,04 герц.

В XVII столетии создатели темперированного строя разделили октаву на двенадцать равных интервалов. Они рассуждали так: если от до до до частота ноты удваивается, то темперированный интервал должен быть ¹²√2. (Умножив двенадцать раз число 1,0595…, получаем искомую двойку.)

Симфоническая музыка выросла из темперации октавы.

Но, понимая, что темперированная гамма – виток спирали, музыковеды вот уже три века не могут уйти от линейных представлений времен позднего Средневековья, хотя все музыканты слышат, что клавишные инструменты почему-то очень плохо звучат рядом со смычковыми.

Можно допустить, что на самом деле темперированный полутон не равен ¹²√2, но только близок к этому числу. И скрипач, и певец, и человек за роялем – все они настроены природой по числу π, а не по квадратным корням. Потому-то, надо полагать, опытные настройщики всегда перестраивают фортепьяно для игры со смычковыми, чуть повышая (по сравнению с эталонной) частоту каждого следующего до (а на самом деле – каждой ноты).

Отказавшись от сведения трансцендентной пространственно-временной гармонии к иррациональной гармонии диагоналей квадратов, мы откажемся от попытки выразить π через √2. И получим другое решение проблемы темперации и другое определение минорной терции: малая (минорная) терция – это диаметр частотного интервала от данной ноты до аналогичной ноты более низкой октавы, то есть серебряное сечение октавы. В этом случае, взяв эталонные значения до I и II октав, мы получим отклонение от камертонного «ля» только в 0,02 герца.

Это значит, что интервал каждой октавы надо расширить на несколько центов.

Ньютон разделил цветовую гамму по соотношениям простейшей фригийской гаммы. С тех пор мы и пользуемся архаичным по сути цветовым строем, очень мало соответствующим реальной «музыке сфер» и просто музыке, а значит, и гармонии вообще.

Серебряное сечение — это математическая константа, выражающая некоторое геометрическое соотношение, выделяемое эстетически. В отличие от золотого сечения, по аллюзии с которым оно названо, серебряное сечение не имеет единого определения.